算法小记 —— 二维矩阵前缀和

适用性

前缀和技巧适⽤于快速、频繁地计算⼀个索引区间内的元素之和

原理

304. 二维区域和检索 - 矩阵不可变 - 力扣（LeetCode）

给定一个二维矩阵 matrix，以下类型的多个请求：

• 计算其子矩形范围内元素的总和，该子矩阵的 左上角 为 (row1, col1) ，右下角 为 (row2, col2) 。

实现 NumMatrix 类：

• NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化
• int sumRegion(int row1, int col1, int row2, int col2) 返回 左上角 (row1, col1) 、右下角 (row2, col2) 所描述的子矩阵的元素 总和 。

方法一

还是类似于一维数组的前缀和，我们将其每一行进行扩展到 n+1 之后利用一维数组前缀和进行计算

对应所需要计算的的列范围为 row1 到 row2，行的范围为 col2+1 到 col1

class NumMatrix {
public:
    vector<vector<int>> preSumMatrix;

    NumMatrix(vector<vector<int>> &matrix) {
        for (auto line: matrix) {
            vector<int> temp = {0};
            for (int i = 1; i <= line.size(); ++i) {
                temp.push_back(temp[i - 1] + line[i - 1]);
            }
            preSumMatrix.push_back(temp);
        }
    }

    int sumRegion(int row1, int col1, int row2, int col2) {
        int sum = 0;
        for (int i = row1; i <= row2; i++) {
            sum += preSumMatrix[i][col2 + 1] - preSumMatrix[i][col1];
        }
        return sum;
    }
};

方法二

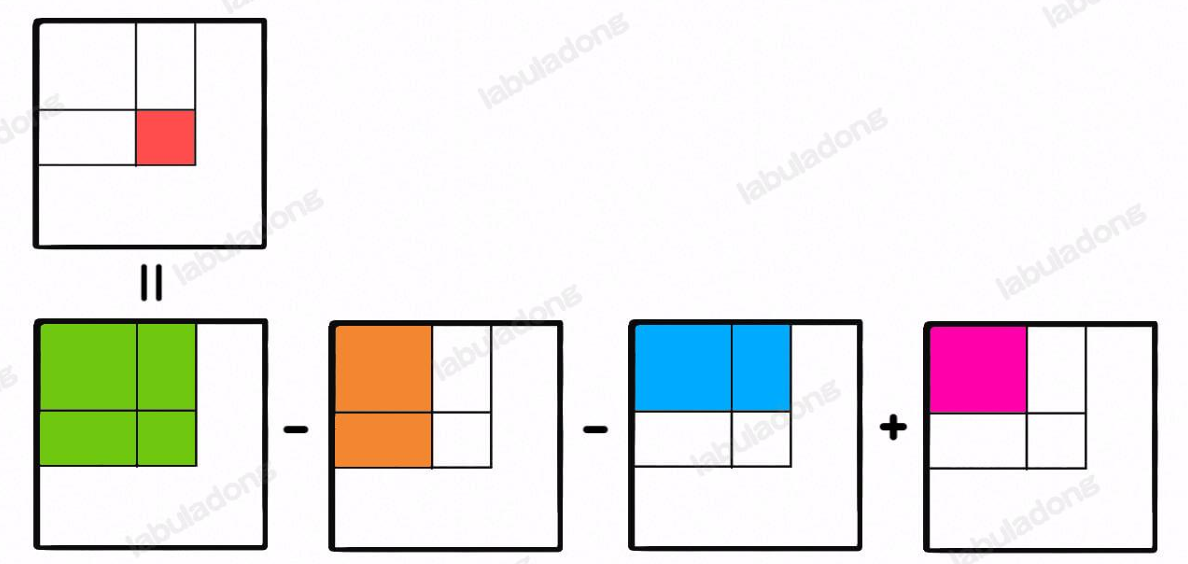
因为任意的子矩阵元素和可以转换为它周边几个大矩阵的元素和的运算

与之对应的我们可以通过计算几个大矩阵的和之后进行运算得到所求子矩阵

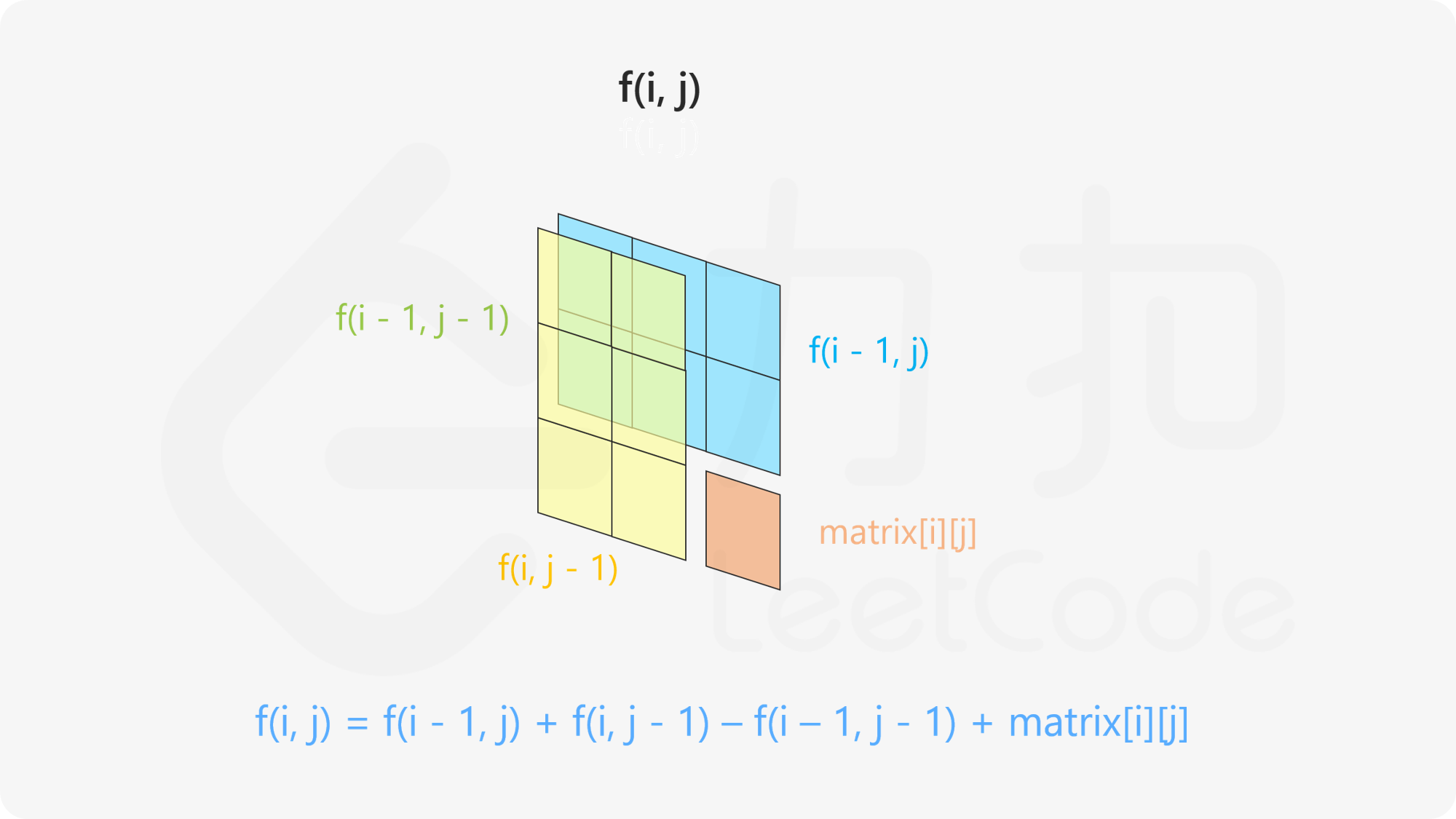
而这四个⼤矩阵有⼀个共同的特点，就是左上⻆都是(0, 0)原点。 那么我们可以维护⼀个⼆维preSumMatrix数组，专⻔记录以原点为顶点的矩阵的元素之和，就可以⽤⼏次加减运算算出任何⼀个⼦矩阵的元素和

class NumMatrix2 {
public:
    //定义：preSum[i][j]记录matrix中子矩阵[0, 0, i-1, j-1]的元素和
    vector<vector<int>> preSumMatrix;

    NumMatrix2(vector<vector<int>> &matrix) {
        int m = matrix.size(), n = matrix[0].size();
        if (m == 0 || n == 0)
            return;
        //构造前缀和矩阵
        preSumMatrix.resize(m + 1, vector<int>(n + 1));
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                //计算每个矩阵[0, 0, i, j]的元素和
                preSumMatrix[i][j] = preSumMatrix[i - 1][j] + preSumMatrix[i][j - 1] - preSumMatrix[i - 1][j - 1] + matrix[i - 1][j - 1];
            }
        }
    }
    
    //计算矩阵[x1, y1, x2, y2]的元素和
    int sumRegion(int x1, int y1, int x2, int y2) {
        //目标矩阵之和由四个相邻矩阵运算获得
        return preSumMatrix[x2 + 1][y2 + 1] - preSumMatrix[x1][y2 + 1] - preSumMatrix[x2 + 1][y1] + preSumMatrix[x1][y1];
    }
};