算法小记 —— 一维数组前缀和

适用性

前缀和技巧适⽤于快速、频繁地计算⼀个索引区间内的元素之和

原理

本质上相当于将一个数组内的元素进行累加，构建一个新的数组用于记录对应下标位置处的累加和

参考图：

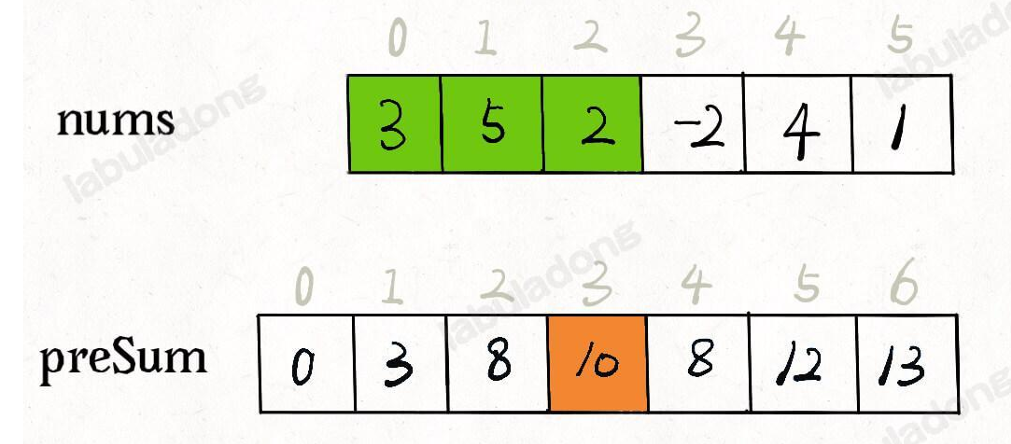
那么我们需要求解某一连续范围内的元素和时，便可以直接转换为新数组对应下标的差

例子

303. 区域和检索 - 数组不可变 - 力扣（LeetCode）

给定一个整数数组 nums，处理以下类型的多个查询:

1. 计算索引 left 和 right （包含 left 和 right）之间的 nums 元素的 和 ，其中 left <= right

实现 NumArray 类：

• NumArray(int[] nums) 使用数组 nums 初始化对象
• int sumRange(int i, int j) 返回数组 nums 中索引 left 和 right 之间的元素的 总和 ，包含 left 和 right 两点（也就是 nums[left] + nums[left + 1] + ... + nums[right] )

#include <bits/stdc++.h>

using namespace std;

class NumArray {
public:
    vector<int> preSum;

    NumArray(vector<int> &nums) {
        preSum.push_back(0);// 构建首项为 0
        for (int i = 1; i <= nums.size(); ++i) {  // 注意等号，不然会少取到 nums 的最后一位
            preSum.push_back(preSum[i - 1] + nums[i - 1]); // 之后求解累加和
        }
    }

    int sumRange(int left, int right) {
        return preSum[right + 1] - preSum[left];
    }
};

int main() {
    vector<int> nums = {3, 5, 2, -2, 4, 1};
    NumArray solution = NumArray(nums);
    cout << solution.sumRange(0, 2) << endl;
    cout << solution.sumRange(2, 5) << endl;
    cout << solution.sumRange(0, 5) << endl;
    return 0;
}