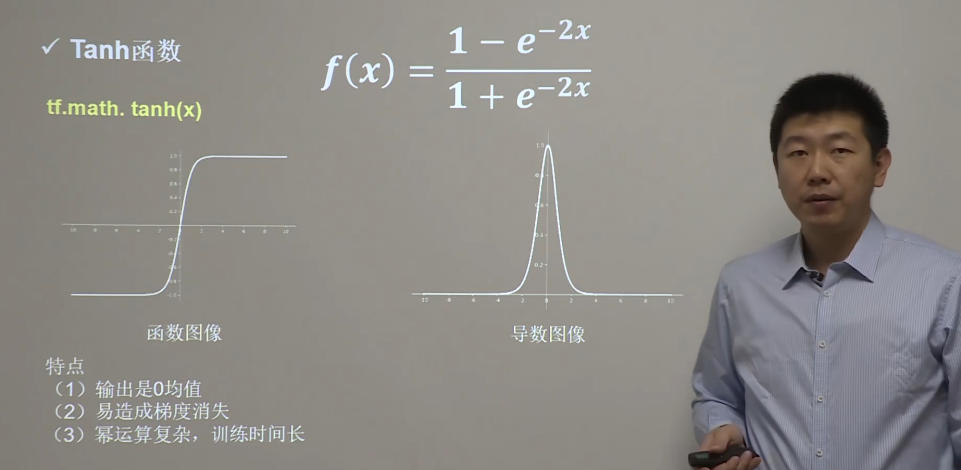Tensorflow入门到入土(轻量版)

前言

本笔记算是对 北京大学 软件与微电子学院 曹健老师 的人工智能实践课程的总结与归纳，收录了课程中的一些函数以及思想方法，方便后来人学习

学习视频链接：人工智能实践：Tensorflow笔记_中国大学MOOC(慕课)

Tensorflow & Numpy 部分函数基础入门

张量概念

维数	阶	名字	例子
0-D	0	标量 scalar	s = 1 2 3
1-D	1	向量 vector	v = [1,2,3]
2-D	2	矩阵 matrix	m = [[1,2,3],[4,5,6],[7,8,9]]
n-D	n	张量 tensor	t = [[[ …]]] (有n个[])

张量可以表示 0 阶到 n 阶数组 (列表)

张量创建

import tensorflow as tf
# 维度：
# 一维 直接写个数
# 二维 用 [行,列]
# 多维 用 [n,m,j,k...]
# 创建全为 0 的张量
tf.zeros(维度)
# 创建全为 1 的张量
tf.ones(维度)
# 创建全为指定值的张量
tf.fill(维度,指定值)

随机数生成

import tensorflow as tf
# 生成正太分布的随机数，默认均值为 0，标准差为 1
tf.random.normal(维度,mean=维度,stddev=标准差)
# 生成截断式正态分布的随机数 (生成的随机数更为集中)
tf.random.truncated_normal(维度,mean=维度,stddev=标准差)

在tf.truncated_normal中如果随机生成数据的取值在（μ-2σ，μ+2σ）之则重新进行生成，保证了生成值在均值附近。
μ：均值 σ：标准差
$$
σ = \sqrt{\frac{\sum_{i=1}^n(x_i-\bar x)^2}{n}}
$$

# 生成均匀分布随机数 [min,max)
tf.random.uniform(维度,minval=最小值,maxval=最大值)
# 返回一个[0,1)之间的随机数
import numpy as np
np.random.RandomState.rand(维度) # 维度为空，返回标量
# 维度eg
rdm = np.random.RandomState(seed=1)
a = rdm.rand() # 返回一共随机标量
b = rdm.rand(2,3) # 返回一共维度为 2 行 3 列的随机数矩阵

常用函数

# 强制tensor转换为该数据类型
tf.cast(张量名,dtype=数据类型)
# 计算张量维度上元素的最小值
tf.reduce_min(张量名)
# 计算张量维度上元素的最大值
tf.reduce_max(张量名)

索引

axis : axis 代表着在一共二维张量或者数组中，可以通过调整 axis 等于 0或者 1 控制执行维度，axis=0时代表跨行，即对列进行操作。当axis=1的时候代表跨列，即对列进行操作，如果不指定 axis 则所有元素参与计算

# 计算张量沿着指定维度的平均值
tf.reduce_mean(张量名, axis=操作轴)
# 计算张量沿着指定维度的和
tf.reduce_sum(张量名, axis=操作轴)

当我们需要返回沿着指定维度最大值或者最小值的索引使，我们可以使用如下函数

tf.argmax(张量名,axis=操作轴)
tf.argmin(张量名,axis=操作轴)
# 找到每一列最大值索引
tf.argmax(x,axis = 0)
# 找到每一行最大值索引
tf.argmax(x,axis = 1)
# 同理于最小值

将变量标记为”可训练“

# 将变量标记为可训练，被标记的变量会在反向传播中记录梯度信息，通常用该函数标记待训练参数
tf.Variable(初始值)

数学运算

需要注意维度相同的张量才可以做四则运算

# 四则运算
tf.add tf.subtract tf.multiply tf.divide
# 平方、次方与开方
tf.square tf.pow tf.sqrt
# 矩阵乘
tf.matmul

将标签与张量进行配对构成数据集

# 切分传入张量的第一维度，生成输入特征/标签对，构建数据集
tf.data.Dataset.from_tensor_slices((输入特征,标签)) # numpy和tensor格式都可以用该语句读入数据

某个函数对指定参数求导计算

# 一般结合with结构记录计算过程，gradient求出张量的梯度
tf.GradientTape()
# 一般采用如下方式计算
with tf.GradientTape() as tape: # 若干个计算过程
    grad = tape.gradient(函数,对谁求导)

枚举 enumerate

返回对应的索引以及元素通常在 for 循环中使用

# enumerate 是 Python 的内建函数，可以遍历每个元素
enumerate(列表名)
# eg:
seq = ['one', 'two', 'three']
for i, element in enumerate(seq):
    print(i, element)
# 输出
0 one
1 two
2 three

标签

对于标签我们常用独热编码表示标签

独热编码：在分类问题中常用独热码做标签，标记类别：1表示是，0表示非

我们可以使用下面的函数，将待转换数据直接转换为独热码形式

# 相当于取对应维度的张量来构成一个对应的张量，其下标使得对应的位置为 1 反之为 0
tf.one_hot(待转换数据,depth=几分类)
# eg
import tensorflow as tf
classes = 2
labels = tf.constant([1, 0, 2])  # 输入的元素值最小为0，最大为2
output = tf.one_hot(labels, depth=classes)
print("result of labels1:", output)
print("\n")
# 输出
result of labels1: tf.Tensor(
[[0. 1.]
 [1. 0.]
 [0. 0.]], shape=(3, 2), dtype=float32)

概率统计

对于分类问题，神经网络完成前向传播，计算出了每种类型的可能性大小，需要输出符合了概率分布时，才可以与独热码的标签作比较
$$
Softmax(y_i)=\frac{e^{y_i}}{\sum ^n_{j=0}e^{y_i}}
$$

# 使输出符合概率分布
tf.nn.softmax(x)
# eg
y = tf.constant([1.01,2.01,-0.66])
y_pro = tf.nn.softmax(y)
print("After softmax,y_pro is:",y_pro)
# 输出
After softmax,y_pro is:tf.Tensor([0.25598174 0.69583046 0.0481878],shape=(3,),dtype=float32)

一般情况下我们将神经网络正向传播后的结果组成张量然后使用该函数对其进行统计概率分布，对于高维我们还可以使用 squeeze 去除大小为 1 的维度

# 't' = [1, 2, 1, 3, 1, 1]
tf.shape(tf.squeeze(t))  # [2, 3]

或者,要删除特定的大小为1的维度：

# 't' = [1, 2, 1, 3, 1, 1]
tf.shape(tf.squeeze(t, [2, 4]))  # [1, 2, 3, 1]

参数自更新

# 赋值操作，更新参数的值并返回
# 调用assign_sub前，先用 tf.Variable定义变量w为可训练（可自更新）
w.assign_sub(w要自减的内容)
# eg
w = tf.Variable(4)
w.assign_sub(1) # w = w - 1 
print(w)
# 输出
<tf.Variable 'Variable:0' shape=() dtype=int32, numpy=3>

条件判别

# 条件语句真返回 A，条件语句假返回 B
tf.where(条件语句,真返回A,假返回B)
# eg
import tensorflow as tf

a = tf.constant([1, 2, 3, 1, 1])
b = tf.constant([0, 1, 3, 4, 5])
c = tf.where(tf.greater(a, b), a, b)  # 若a>b，返回a对应位置的元素，否则返回b对应位置的元素
print("c:", c)
# 输出
c:tf.Tensor([1 2 3 4 5], shape=(5,), dtype=int32)

垂直叠加

# 将两个数组按垂直方向叠加
np.vstack((数组1,数组2)) # numpy 中的方法

网格坐标点生成

# 生成等间隔数值点 [起始值,结束值)
np.mgrid[起始值:结束值:步长,起始值:结束值:步长,...]
# 将 x 变为一位数组，即把 . 前变量拉直
x.ravel()
# 使返回的间隔数值点配对
np.c_[数组1,数组2,...]
# 通常上述三个方法一起使用

神经网络(NN)复杂度

我们对于神经网络的复杂度统计只统计具有运算能力的层，同时在输入层和输出层中间的所有层都称之为隐藏层

学习率

指数衰减学习率

可以先用较大的学习率，快速得到最优解，然后逐步减小学习率，使模型在训练后期稳定
$$
指数衰减学习率 = 初始学习率*学习率衰减率^{\frac{当前轮数}{多少轮衰减一次}}
$$

初始学习率 与 学习衰减率 与 多少轮衰减一次 为超参数

激活函数

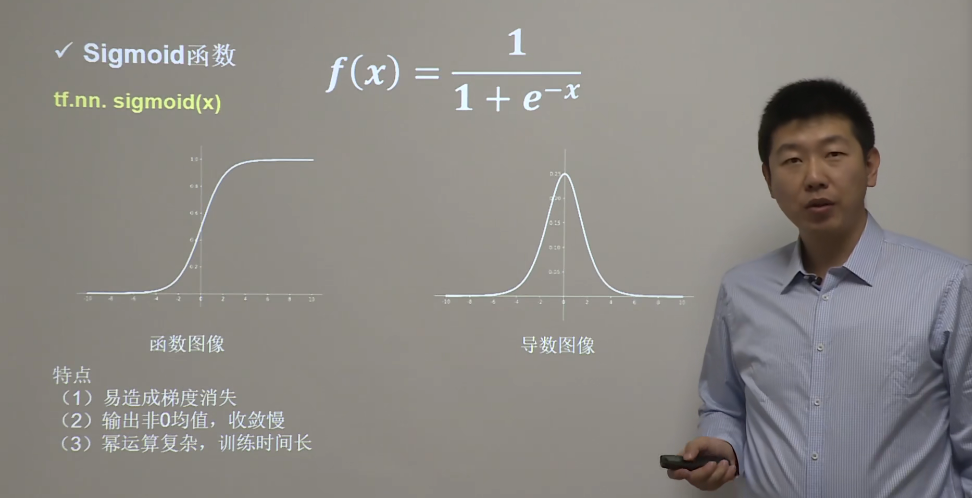
Sigmoid 函数

Sigmoid函数也叫Logistic函数，用于隐层神经元输出，取值范围为(0,1)，它可以将一个实数映射到(0,1)的区间，可以用来做二分类。在特征相差比较复杂或是相差不是特别大时效果比较好。sigmoid是一个十分常见的激活函数，函数的表达式如下：
$$
f(x)=\frac{1}{1+e^{-x}}
$$

tf.nn.sigmoid(x)

在什么情况下适合使用 Sigmoid 激活函数呢？

• Sigmoid 函数的输出范围是 0 到 1。由于输出值限定在 0 到1，因此它对每个神经元的输出进行了归一化；
• 用于将预测概率作为输出的模型。由于概率的取值范围是 0 到 1，因此 Sigmoid 函数非常合适；
• 梯度平滑，避免「跳跃」的输出值；
• 函数是可微的。这意味着可以找到任意两个点的 sigmoid 曲线的斜率；
• 明确的预测，即非常接近 1 或 0。

Sigmoid 激活函数存在的不足：

• 梯度消失：注意：Sigmoid 函数趋近 0 和 1 的时候变化率会变得平坦，也就是说，Sigmoid 的梯度趋近于 0。神经网络使用 Sigmoid 激活函数进行反向传播时，输出接近 0 或 1 的神经元其梯度趋近于 0。这些神经元叫作饱和神经元。因此，这些神经元的权重不会更新。此外，与此类神经元相连的神经元的权重也更新得很慢。该问题叫作梯度消失。因此，想象一下，如果一个大型神经网络包含 Sigmoid 神经元，而其中很多个都处于饱和状态，那么该网络无法执行反向传播。
• 不以零为中心：Sigmoid 输出不以零为中心的,，输出恒大于0，非零中心化的输出会使得其后一层的神经元的输入发生偏置偏移（Bias Shift），并进一步使得梯度下降的收敛速度变慢。
• 计算成本高昂：exp() 函数与其他非线性激活函数相比，计算成本高昂，计算机运行起来速度较慢。

Tanh 函数

Tanh 激活函数又叫作双曲正切激活函数（hyperbolic tangent activation function）。与 Sigmoid 函数类似，Tanh 函数也使用真值，但 Tanh 函数将其压缩至-1 到 1 的区间内。与 Sigmoid 不同，Tanh 函数的输出以零为中心，因为区间在-1 到 1 之间。

函数表达式：
$$
f(x)=\frac{1-e^{-2x}}{1+e^{-2x}}
$$

tf.math.tanh(x)

在实践中，Tanh 函数的使用优先性高于 Sigmoid 函数。负数输入被当作负值，零输入值的映射接近零，正数输入被当作正值：

• 当输入较大或较小时，输出几乎是平滑的并且梯度较小，这不利于权重更新。二者的区别在于输出间隔，tanh 的输出间隔为 1，并且整个函数以 0 为中心，比 sigmoid 函数更好；
• 在 tanh 图中，负输入将被强映射为负，而零输入被映射为接近零。

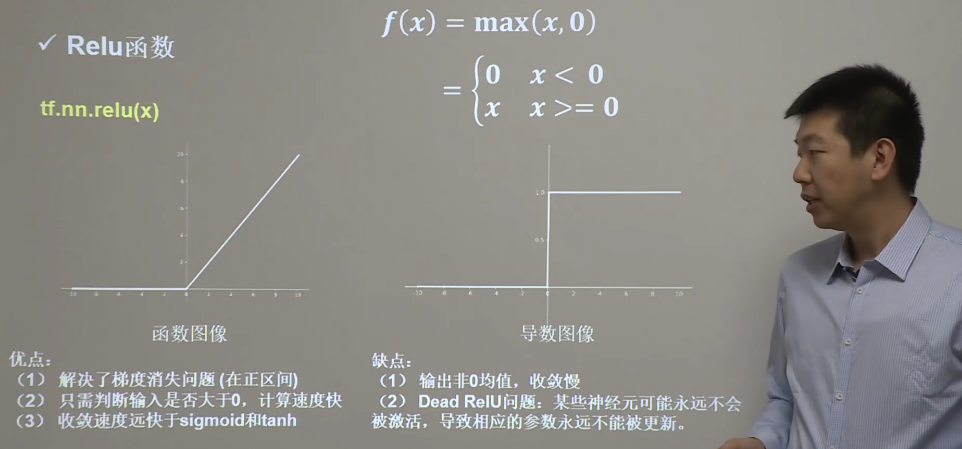
Relu 函数

ReLU函数又称为修正线性单元（Rectified Linear Unit），是一种分段线性函数，其弥补了sigmoid函数以及tanh函数的梯度消失问题，在目前的深度神经网络中被广泛使用。ReLU函数本质上是一个斜坡（ramp）函数，公式及函数图像如下：
$$
f(x)=max(x,0)\\ \ \ \ \ \ \ \ \ \ \ \ \ =\begin{cases} 0\ \ \ \ \ x<0 \x\ \ \ \ \ x>=0 \end{cases}
$$

tf.nn.relu(x)

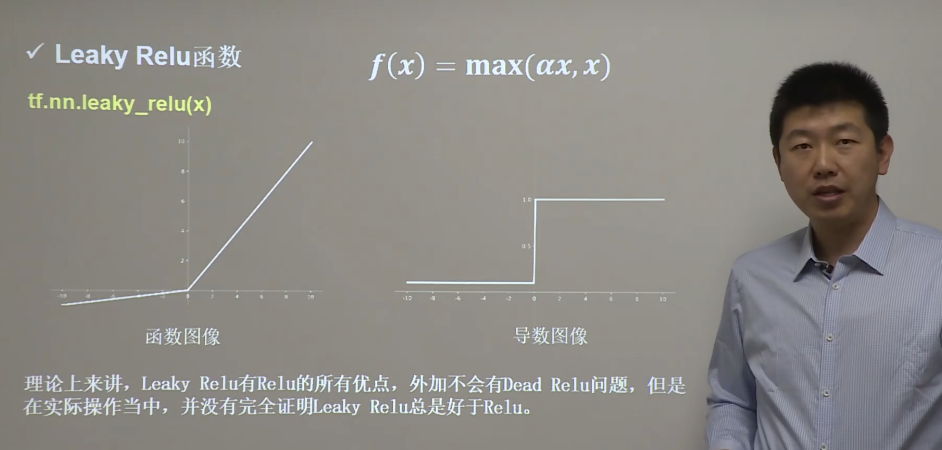
Leaky Relu 函数

为了解决 ReLU 激活函数中的梯度消失问题，当 x < 0 时，我们使用 Leaky ReLU —— 该函数试图修复 dead ReLU 问题。

函数表达式以及图像如下：
$$
f(x)=max(ax,x)
$$

tf.nn.leaky_relu(x)

softmax

Softmax 是用于多类分类问题的激活函数，在多类分类问题中，超过两个类标签则需要类成员关系。对于长度为 K 的任意实向量，Softmax 可以将其压缩为长度为 K，值在（0，1）范围内，并且向量中元素的总和为 1 的实向量。

函数表达式如下：
$$
S_i=\frac{e^i}{\sum_je^j}
$$

Softmax 激活函数的不足：

• 在零点不可微；
• 负输入的梯度为零，这意味着对于该区域的激活，权重不会在反向传播期间更新，因此会产生永不激活的死亡神经元。

一些建议 —— 对于初学者

1. 首选relu激活函数
2. 学习率设置较小值
3. 输入特征标准化，即让输入特征满足以 0 为均值，1 为标准差的正态分布
4. 初始参数中心化，即让随机生成的参数满足以 0 为均值，$\sqrt{\frac{2}{当前层输入特征个数}}$为标准差的正态分布

损失函数

损失函数(loss)：预测值(y)与已知答案(y_)的差距

NN优化目标 -> loss 最小

mse 损失函数

$$
MSE(y,y_)=\frac{\sum_{k=0}^{n}(y-y_)^2} n
$$

loss_mse = tf.reduce_mean(tf.square(y-y_))

自定义损失函数

$$
loss(y_,y)=\sum_n f(y_,y)
$$

y_ : 标准答案数据集的 y : 预测答案计算出的

即我们可以自己定义对应不同情况下的损失率，对于不同的情况下定义相应的 f(y_,y)

交叉熵 CE

其表示两个概率分布之间的距离
$$
H(y_,y)=-\sum y*\ln y
$$

tf.losses.categorical_crosseentropy(y_,y)

当交叉熵越小时，对应的预测更为准确

一般来说我们通常先将输出通过 softmax 转换为符合概率分布的结果，再计算 y 与 y_ 的交叉熵损失函数

tf.nn.softmax_cross_entropy_with_logits(y,y_)
# 等价于下面两条语句
y_pro = tf.nn.softmax(y)
tf.losses.catgorical_crossentropy(y_,y_pro)

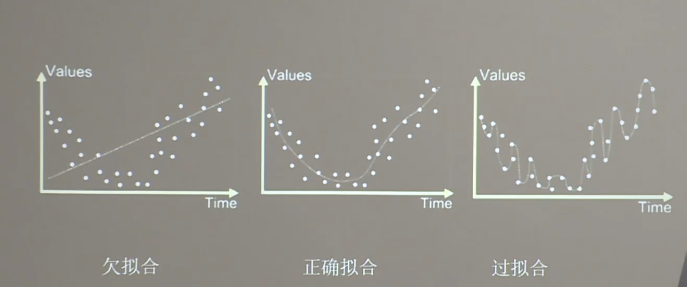
欠拟合与过拟合

对于欠拟合我们有如下解决方法：

1. 增加输入特征选项

2. 增加网络参数

3. 减少正则化参数

对于过拟合我们有如下方法：

1. 数据清洗
2. 增大训练集
3. 采用正则化
4. 增大正则化参数

正则化：在损失函数中引入模型复杂度指标，通过给 w 添加权值，而弱化训练数据的噪声 (一般不正则化 b)

参数优化器

优化器是引导神经网络更新参数的工具

我们定义如下参数：待优化参数 w，损失函数 loss，学习率 Lr，每次迭代一个 batch，t 表示当前 batch 迭代的总次数

1. 计算 t 时刻损失函数关于当前参数的梯度 $g_t=\nabla loss = \frac {\partial loss}{\partial(w_t)}$
2. 计算 t 时刻一阶动量$m_t$和二阶动量$V_t$
3. 计算 t 时刻下降梯度$\eta_t =Lr *\frac{m_t}{\sqrt V_t}$
4. 计算 t+1 时刻下降梯度$w_{t+1} =w_t-\eta_t=w_t-Lr *\frac{m_t}{\sqrt V_t}$

一阶动量：与梯度相关的函数

二阶动量：与梯度平方相关的函数

对于不同的优化器，实质上只是定义了不同的一阶动量和二阶动量公式

SGD 优化器

SGD是最常用的随机梯度下降法，当不含动量时其定义了如下动量计算方式

$g_t$ ：对应的各时刻梯度值

SGDM 优化器

在 SGD 的基础上增加一阶动量

$m_t$ ： 表示各时刻梯度方向的指数滑动平均值

# 超参数设置
m_w, m_b = 0, 0
beta = 0.9 # 经验值是 0.9
# sgd-momentun  
m_w = beta * m_w + (1- beta) * grads[0]
m_b = beta * m_b + (1- beta) * grads[1]
w1.assign_sub(lr * m_w)
b1.assigen_sub(lr * m_b)

Adagrad 优化器

其在SGD的基础上增加二阶动量

# 超参数设置
v_w, v_b = 0, 0
# adagrad
v_w += tf.square(grads[0])
v_b += tf.square(grads[1])
w1.assign_sub(lr * grads[0] / tf.sqrt(v_w))
b1.assign_sub(lr * grads[0] / tf.sqrt(v_b))

RMSProp 优化器

在SGD的基础上增加二阶动量

# 超参数设置
v_w, v_b = 0, 0
beta = 0.9
# RMSProp
v_w = beta * v_w + (1- beta) * tf.square(grads[0])
v_b = beta * v_b + (1- beta) * tf.square(grads[1])
w1.assign_sub(lr * grads[0] / tf.sqrt(v_w))
b1.assign_sub(lr * grads[0] / tf.sqrt(v_b))

Adam 优化器

同时结合了SGDM一阶动量和RMSProp二阶动量

# 超参数设置
m_w, m_b = 0, 0
v_w, v_b = 0, 0
beta1, beta2 = 0.9, 0.999
delta_w, delta_b = 0, 0
global_step = 0
# 训练过程
for epoch in range(epoch):  # 数据集级别的循环，每个epoch循环一次数据集
    for step, (x_train, y_train) in enumerate(train_db):  # batch级别的循环 ，每个step循环一个batch
		global_step += 1
		...
# Adam
		m_w = beta1 * m_w + (1 - beta1) * grads[0]
        m_b = beta1 * m_b + (1 - beta1) * grads[1]
        v_w = beta2 * v_w + (1 - beta2) * tf.square(grads[0])
        v_b = beta2 * v_b + (1 - beta2) * tf.square(grads[1])

        m_w_correction = m_w / (1 - tf.pow(beta1, int(global_step)))
        m_b_correction = m_b / (1 - tf.pow(beta1, int(global_step)))
        v_w_correction = v_w / (1 - tf.pow(beta2, int(global_step)))
        v_b_correction = v_b / (1 - tf.pow(beta2, int(global_step)))

        w1.assign_sub(lr * m_w_correction / tf.sqrt(v_w_correction))
        b1.assign_sub(lr * m_b_correction / tf.sqrt(v_b_correction))

梯度下降

损失函数

$$
MSE(y,y_)=\frac{\sum_{k=0}^{n}(y-y_)^2} n
$$
上述特征x * w + b = y的过程被称为正向传播，而我们的目的是找到一组参数w和b，使得损失函数最小

梯度下降法:沿损失函数梯度下降的方向，寻找损失函数的最小值，得到最优参数的方法。

学习率(Lr):当学习率设置的过小时，收敛过程将变得分缓慢。而当学习率设置的过大时，梯度可能会在最小值附近来回震荡,甚至可能无法收敛。

梯度下降算法

$$
W_{t+1} =W_t-Lr*\frac{\partial loss}{\partial W_t}
$$

$$
b_{t+1}=b-Lr*\frac{\partial loss}{\partial b_t}
$$

$$
W_{t+1}*x+b_{t+1}\rightarrow y
$$

反向传播:从S后向前，逐层求损失函数对每层神经元参数的偏导数，迭代更新所有参数

Keras 搭建神经网络

Keras是tensorflow的一个模块，用于快速搭建神经网络

import tensorflow as tf
model = tf.keras.models.Sequential([网络结构]) # 描述各层网络
# 网络结构举例
# 拉直层
tf.keras.layers.Flatten()
# 全链接层
tf.keras.layers.Dense(神经元个数,activation="激活函数",kernel_regularizer=正则化方式)
# activation可选: relu、softmax、sigmoid、tanh
# kernel_regularizer可选: tf.keras.regularizers.l1()、tf.keras.regularizers.l2()
# 卷积层
tf.keras.layers.Conv2D(filters=卷积核个数,kernel_size=卷积核尺寸,strides=卷积步长,padding="vaild" or "same")
# LSTM层
tf.keras.layers.LSTM()

配置神经网络方法

model.compile(optimizer=优化器,loss=损失函数,metrics=["准确率"])
# 优化器可选项
'sgd' or tf.keras.optimizers.SGD(lr=学习率,momentum=动量参数)
'adagrad' or tf.keras.optimizers.Adagrad(lr=学习率)
'adadelta' or tf.keras.optimizers.Adadelta(lr=学习率)
'adam' or tf.keras.optimizers.Adam(lr=学习率,beta_1=0.9,beta_2=0.999)
# loss 可选项
'mse' or tf.keras.losses.MeanSquaredError()
'sparse_categorical_crossentropy' or tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False) # 设置损失函数时常用，from_logits参数用于询问是否使用原始输出，即没有经过概率分布的输出
# Metrics 可选项
'accuracy' : y_ 与 y 都是数值，如:y_=[1],y=[1]
'categorical_accuracy' : y_ 与 y 都是独热码(概率分布)，如:y_=[0,1,0],y=[0.235,0.648,0.117]
'sparse_categorical_accuracy' : y_是数值，y是独热码(概率分布)，如:y_=[1],y=[0.235,0.648,0.117]

初学建议直接使用字符串形式的参数，对于熟悉后可以查询相关文档后使用后者，修改相关的超参数

执行训练

model.fit(训练集的输入特征,训练集的标签,
         batch_size= , epochs= ,
         validation_data=(测试机的输入特征,测试集的标签),
         validation_freq=多少次epoch测试一次)
# 或者
model.fit(训练集的输入特征,训练集的标签,
         batch_size= , epochs= ,
         validation_split=从训练集划分多少比例给测试集,
         validation_freq=多少次epoch测试一次)

网络参数和结构统计

model.summary()

自制数据集

需要我们设计一共函数来将我们的数据集进行读入，对此我们可能需要创建对应的文件或者是对于对应的目录下的文件进行检测，对此我们需要导入 os，利用其内置库进行读写与判断,此处以读入图片进行训练为例子：

import os
from PIL import Image
import numpy as np
import tensorflow as tf

train_path = XXX
train_txt = XXX
x_train_savepath = XXX
y_train_savepath = XXX

test_path = XXX
test_txt = XXX
x_test_savepath = XXX
y_test_savepath = XXX

def GenerateData(path,txt):
    f = open(txt,'r')
    data = f.readlines()
    f.close()
    x, y_=[], []
    for content in data:
        value = content.split() # 以空格进行分割数据
        img_path = path + value[0] # 构建图片位置
        img = Image.open(img_path) # 打开图片
        img = np.array(img.convert('L')) # 将图片转为8位宽灰度值，通过np.array进行读入
        img  = img / 256 # 数据归一化
        x.append(img)
        y_.append(value[1])
        print("loading: " + img_path) # 提示信息
        
    x = np.array(x) # 变为np.array格式
    y_ = np.array(y_) # 变为np.array格式
    y_ = y_.astype(np.int64) # 变为np.int64整型
    return x,y_

def check(x_train_savepath,y_train_savepath,x_test_savepath,y_test_savepath):
    if os.path.exists(x_train_savepath) and os.path.exists(y_train_savepath) 
    and os.path.exists(x_test_savepath) and os.path.exists(y_test_savepath):
        
    print('-------------Load Datasets-----------------')
    
    x_train_save = np.load(x_train_savepath)
    y_train = np.load(y_train_savepath)
    x_test_save = np.load(x_test_savepath)
    y_test = np.load(y_test_savepath)
    x_train = np.reshape(x_train_save, (len(x_train_save), 28, 28))
    x_test = np.reshape(x_test_save, (len(x_test_save), 28, 28))
else:
    print('-------------Generate Datasets-----------------')
    
    x_train, y_train = generateds(train_path, train_txt)
    x_test, y_test = generateds(test_path, test_txt)

    print('-------------Save Datasets-----------------')
    
    x_train_save = np.reshape(x_train, (len(x_train), -1)) # 将数组拉成一维数组
    x_test_save = np.reshape(x_test, (len(x_test), -1)) # 将数组拉成一维数组
    np.save(x_train_savepath, x_train_save)
    np.save(y_train_savepath, y_train)
    np.save(x_test_savepath, x_test_save)
    np.save(y_test_savepath, y_test)

数据增强

数据增强可以帮助我们扩充数据集，对于图像而言就是简单的形变，可以用于应对图片拍照角度的不同而照成的一定形变

image_gen_train = tf.keras.preprocessing.image.ImageDataGenerator(
	rescale=所有数据将乘以该数值, # 当为图像的时候，分母为255时，可以归至 0~1 的区间
	rotation_range=随机旋转角度数范围,
    width_shift_range=随机宽度偏移量, 
    height_shift_range =随机高度偏移量,
	horizontal_flip=是否随机水平翻转 # True or False
	zoom_range =随机缩放的范围[1-n,1+n] )  # eg： 0.5

image_gen_train.fit(x_train)

断点续训

断点续训可以让我们训练不用每次都从头开始训练，而不用每次重头开始训练

# 读取模型
load_weights(路径文件名) # .ckpt 文件
# 保存模型
tf.keras.callbacks.ModelCheckpoint(
	filepath=文件名,
	save_weights_only=True/False,
	save_best_only=True/False)

history = model.fit(callbacks=[cp_callback])

参数提取

我们可以把参数存入文本，观察训练的参数，我们可以采用print进行输出，但是当输出信息过长时中间的部分会被省略号所替代，我们可以通过下面的函数把我们模型中可以训练的参数进行打印

# 返回模型中可训练的参数
model.trainable_variables
# 设置print输出格式
np.set_printoptions(threshold=超过多少省略显示) # np.inf 表示无限大
# eg
np.set_printoptions(threshold=np.inf)
print(model.trainable_variables)
file = open('./weights.txt','w')
for v in model.trainable_variables:
    file.write(str(v.name)+'\n')
    file.write(str(v.shape)+'\n')
    file.write(str(v.numpy())+'\n')
    
file.close()

acc/loss 可视化

在训练过程中其实对训练集、测试集、训练集准确率、测试集准确率都有着对应的记录，我们可以将其进行提取，以可视化的方式来观察我们训练的效果

# 提取方式
history = model.fit(训练集的输入特征,训练集的标签,
         batch_size= , epochs= ,
         validation_split=从训练集划分多少比例给测试集,
         validation_freq=多少次epoch测试一次)
# history 
训练集 loss : loss
测试集 loss : val_loss
训练集准确率 : sparse_categorical_accuracy
测试集准确率 : val_sparse_categorical_accuracy

当我们拿到对应的数据后我们便可以用 matplotlib 进行绘图

#需要导入下面的包
from matplotlib import pyplot as plt 
# 绘图
acc = history.history['sparse_categorical_accuracy'] # 训练集准确率
val_acc = history.history['val_sparse_categorical_accuracy'] # 测试集准确率
loss = history.history['loss'] # 训练集 loss
val_loss = history.history['val_loss'] # 测试集 loss

# plt.subplot 将图像分为一行两列
plt.subplot(1, 2, 1) # 划出第一列
plt.plot(acc, label='Training Accuracy') # 设置图标题
plt.plot(val_acc, label='Validation Accuracy')
plt.title('Training and Validation Accuracy')
plt.legend() # 画出图例

plt.subplot(1, 2, 2) # 划出第二列
plt.plot(loss, label='Training Loss')
plt.plot(val_loss, label='Validation Loss')
plt.title('Training and Validation Loss')
plt.legend()
plt.show()

应用

之前所用到的东西都不同于其他的程序，仅仅有了一个网络，但是要想真正运行起来需要我们编写一个应用程序，可以将我们的输入进行预测，给出一共预测的结果，在 tensorflow 中有对应的函数将我们的前向传播进行执行应用给出一个对应的预测

# 返回前向传播计算结果
predict(输入特征,batch_size=整数)
# eg
model = tf.keras.models.Sequential([
	tf.keras.layers.Flatten(),
	tf.keras.layers.Dense(128,actvation='relu'),
	tf.keras.layers.Dense(10,activation='softmax')
]) # 复现模型 —— 前向传播
model.load_weights(model_save_path) # 加载参数
result = model.predict(x_predict) # 预测结果

卷积神经网络

卷积就是特征提取器：卷积->批标准化->激活->池化

卷积神经网络便是借助卷积核提取特征后送入全连接网络

卷积计算过程

卷积计算那是一种有效提取图像特征的方法

一般会用一个正方形的卷积核,按指定步长,在输入特征图上滑动，遍历输入特征图中的每个像素点。每一个步长，卷积核会与输入特征图出现重合区域，重合区域对应元素相乘、求和再加上偏置项得到输出特征的一个像素点

输入特征图的深度(channel数)，决定了当前层卷积核的深度;当前层卷积核的个数，决定了当前层输出特征图的深度。

对应元素相乘之后求和再加上对应的偏置项 b

感受野(Receptive Field)

卷积神经网络各输出特征图中的每个像素点，在原始输入图片上映射区域的大小。

全零填充(Padding)

卷积计算保持输入特征图的尺寸不变可以使用全零填充

卷积核计算

tf.keras.layers.Conv2D(
	filters=卷积核个数,
	kernel_size=卷积核尺寸, # 正方形写核长整数，或(核高 h ，核宽 w)
	strides=滑动步长, # 横纵向相同写步长整数，或(纵向步长 h ，横向步长 w)，默认为 1
    padding="same" or "valid" # 使用全零填充是"same"，不使用是"valid"(默认)
    activation="relu" or "sigmoid" or "softmax" or "tanh" # 如有批标准化此处不写
    input_shape=(高,宽,通道数) # 输入特征图维度，可省略
)
# eg
model = tf.keras.models.Sequential([
    Conv2D(6,5,padding='valid',activation='sigmoid'),
    MaxPool2D(2,2),
    Conv2D(6,(5,5),padding='valid',activation='sigmoid'),
    MaxPool2D(2,(2,2)),
    Conv2D(filters=6, kernel_size=(5,5),padding='valid',activation='sigmoid'),
    MaxPool2D(pool_size=(2,2),strides=2),
    Flatten(),
    Dense(10,activation='softmax')
])

批标准化(BN)

标准化：使数据符合 0 均值， 1 为标准差的分布

批标准化：对一小批数据(batch)进行标准化处理，常用在卷积和激活之间

卷积 -> 批标准化 -> 激活

tf.keras.layers.BatchNormalizaton()
# eg
model = tf.keras.models.Sequential([
    Conv2D(filters=6,kernel_size=(5,5),padding='same'),# 卷积层
    BatchNormalization(), # BN 层
    Activation('relu'), # 激活层
    MaxPool2D(pool_size=(2,2),strides=2,padding='same'), # 池化层
    Dropout(0.2) # dropout 层
])

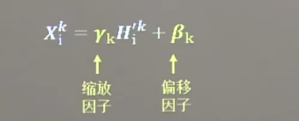
批标准化操作会让每个像素点进行减均值除以标准差的自更新计算，在经过标准化操作后将其重新拉回到 0 均值，数据更集中于激活函数的线性区域，提升了激活函数对输入数据的区分力

但是简单的数据标准化使特征数据完全满足了正态分布，集中在激活函数中间的线性区域，使激活函数失去了非线性特性，因此BN操作中为每个卷积核引入了两个可训练参数用于控制缩放和偏移

在反向传播中使其一起被优化，进而优化数据的分布

池化

池化操作用于减少卷积神经网络中特征数据量，最大值池化可提取图片纹理，均值池化可保留背景特征。

最大池化：将池化核中的最大值进行保留

tf.keras.layers.MaxPool2D(
	pool_size=池化核尺寸, # 正方形写核长整数，或(核高 h ，核宽 w)
    strides=池化步长, # 横纵向相同写步长整数，或(纵向步长 h ，横向步长 w)，默认为 pool_size
    padding="same" or "valid" # 使用全零填充是"same"，不使用是"valid"(默认)
)

均值池化：将池化核中的数据的平均值进行替代

tf.keras.layers.AveragePooling2D(
	pool_size=池化核尺寸, # 正方形写核长整数，或(核高 h ，核宽 w)
    strides=池化步长, # 横纵向相同写步长整数，或(纵向步长 h ，横向步长 w)，默认为 pool_size
    padding="same" or "valid" # 使用全零填充是"same"，不使用是"valid"(默认)
)

舍弃

在神经网络训练时，将将隐藏层的一部分神经元按照一定概率从神经网络中暂时舍弃。神经网络使用时，被舍弃的神经元恢复链接。

tf.keras.layers.Dropout(舍弃的概率)

循环神经网络

使用循环神经网络实现连续数据的预测，即借助循环核提取时间特征后送入全链接网络

循环核

参数时间共享，循环层提取时间信息

循环计算层

循环计算层向输出方向生长

tf.keras.layers.SimpleRNN(记忆体个数,activation='激活函数',return_sequences=是否每个时刻输出ht到下一层) # ht 为记忆体内存储的状态信息
# activation 不写默认使用tanh
# return_sequences=True 各时间步输出ht
# return_sequences=False 仅最后时间步输出ht (默认)
# eg
SimpleRNN(3,return_sequences=True)

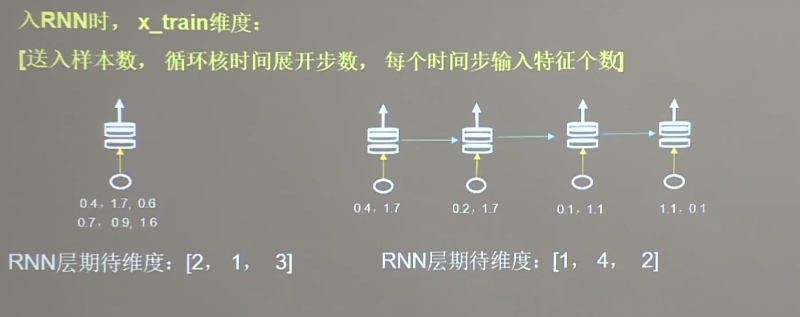
入RNN时，x_train维度：[送入样本数,循环核时间展开步数,每个时间步输入特征个数]

Embedding 单词编码

独热码:数据量大过于稀疏，映射之间是独立的，没有表现出关联性

Embedding:是一种单词编码方法，用低维向量实现了编码，这种编码通过神经网络训练优化，能表达出单词间的相关性。

tf.keras.layers.Embedding(词汇表大小,编码维度)

编码维度就是用几个数字表达一个单词

对1-100进行编码，[4]编码为[0.25，0.1,0.11]

例:tf.keras.layers.Embedding(100,3)

入Embedding时， x_train维度:[送入样本数，循环核时间展开步数]

LSTM 长短记忆网络

$W_i$、$b_i$、$W_f$、$b_f$、$W_o$、$b_o$均为待训练参数，再Sigmoid函数的作用下归一化

门限取值范围为(0,1)

tf.keras.layers.LSTM(记忆体个数,return_sequences=是否返回输出)
# return_sequences=True 各时间步输出ht
# return_sequences=False 仅最后时间输出ht(默认)

GRU 网络

GRU使记忆体 ht 融合了长期记忆和短期记忆

tf.keras.layers.GRU(记忆体个数,return_sequences=是否返回输出)
# return_sequences=True 各时间步输出ht
# return_sequences=False 仅最后时间输出ht(默认)