CSAPP - Data Lab

前言

看到网上对这个实验讲解的不是很详细，个人将其中的一些部分进行了细化方便大家理解与学习，如有不对处还请多多指正。

第一题

用&和~在 14 个字符以内实现异或

1
2
3
4
5
6
7
8
9
10
/* 
 * bitXor - x^y using only ~ and & 
 *   Example: bitXor(4, 5) = 1
 *   Legal ops: ~ &
 *   Max ops: 14
 *   Rating: 1
 */
int bitXor(int x, int y) {
  return 2;
}

求解方式有如下 3 种方式：

1
2
3
4
a^b=
= (a|b)&(~a|~b)
= ~(~a&~b)&~(a&b)
= (a&~b)|(~a&b)

可以用这三种方式表示异或操作，具体的推导可以自行Google。答案如下：

1
return ~(~a&~b)&~(a&b);

第二题

题目要求返回最小二进制补码整数，

1
2
3
4
5
6
7
8
9
10
11
/* 
 * tmin - return minimum two's complement integer 
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 4
 *   Rating: 1
 */
int tmin(void) {

  return 2;

}

我们已知最小的二进制补码数是-2147483648其对应的二进制位是1000000...，所以我们直接将 1 进行左移即可得到。答案如下：

1
return 1<<31;

第三题

题目要求如果是补码的最大数返回 1 ，否则返回 0

1
2
3
4
5
6
7
8
9
10
/*
 * isTmax - returns 1 if x is the maximum, two's complement number,
 *     and 0 otherwise 
 *   Legal ops: ! ~ & ^ | +
 *   Max ops: 10
 *   Rating: 1
 */
int isTmax(int x) {
  return 2;
}

我们知道011111.....表示的是补码的最大二进制位，如果我们对其加 1 可以得到10000000....再取一次反便可以得到原来的最大补码。同时由于一个数异或本身为 0 ，我们便可以利用个性质来代替等号的判断，于是我们有对应的如下思路：

1
~ ( a + 1 ) ^ a == 0 ? 1 : 0

题目中并没有允许?:的使用，于是我们可以换一种方式来实现这个过程：

1
return ! ( ~ ( a + 1 ) ^ a );

上述的结果并不完全正确，如果我们输入的数字是1111111...那么再经过上述操作过后，会再次变回该数字，因此我们要判断这个特例

1111… + 1 = 0000…
~ 0000… = 1111…

我们这里引入一个概念规格化数据：!! x

1
2
3
4
//我们对一个数进行两次取反，如果一个数是不为 0 的数，两次取反后返回值是 1 ，如果该数是 0 ，则返回的仍为 0
!! 123 = 1
!! -1 = 1
!! 0 = 0

同时我们利用&运算符的特性，一个数与 0 进行与运算的结果都是 0 ，来判断特殊数据1111...，我们构造如下式子来进行判断特殊数据：

1
!! (( x + 1 ) ^ 0x0 )

如果输入值是1111...那么其值是 0 ，其他情况下返回值为 1

于是我们可以写出对应解：

1
return ! ( ~ ( a + 1 ) ^ a ) & !! (( x + 1 ) ^ 0x0 );

第四题

题目要求判断所有二进制偶数位是否都为 1 ，如果是返回 1 否则返回 0

1
2
3
4
5
6
7
8
9
10
11
12
/* 
 * allOddBits - return 1 if all odd-numbered bits in word set to 1
 *   where bits are numbered from 0 (least significant) to 31 (most significant)
 *   Examples allOddBits(0xFFFFFFFD) = 0, allOddBits(0xAAAAAAAA) = 1
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 12
 *   Rating: 2
 */
int allOddBits(int x) {
  return 2;
}

我们从题目中了解到最大长度的二进制位长 32 ，我们注意到：一个特殊的数据101010....与一个数进行&运算得到的结果如果与101010....本身异或等于 0 时则证明了该数的二进制偶数位上全是 1 。

对此我们需要101010....来帮助我们进行判断，但是题目中不允许我们直接定义，于是我们将A ( 1010 ) 进行变换得到0xAAAAAAAA

1
2
3
4
int A = 0xA			//4
int AA = A | A << 4		//8
int AAA = AA | AA << 8		//16
int AAAA = AAA | AAA << 16		//32

通过上述方式我们构造出来了0xAAAAAAAA，于是我们可以进行相应的运算了，答案如下：

1
2
3
4
5
int A = 0xA			//4
int AA = A | A << 4		//8
int AAA = AA | AA << 8		//16
int AAAA = AAA | AAA << 16		//32
return !((AAAA&x) ^ AAAA)

第五题

题目要求返回输入数据的负数

1
2
3
4
5
6
7
8
9
10
/* 
 * negate - return -x 
 *   Example: negate(1) = -1.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 5
 *   Rating: 2
 */
int negate(int x) {
  return 2;
}

一个数x，-x为其补码，所以我们对x取反码后加一，得到的便是其所对应的负数

A + ~A = -1 和 A + neg A =0 利用这两个式子我们可以得到 neg A = ~A + 1

所以答案为：

1
return ~ x + 1

第六题

题目要求如果输入的ASCII在字符0 - 9之间就返回 1 否则返回 0

1
2
3
4
5
6
7
8
9
10
11
12
/* 
 * isAsciiDigit - return 1 if 0x30 <= x <= 0x39 (ASCII codes for characters '0' to '9')
 *   Example: isAsciiDigit(0x35) = 1.
 *            isAsciiDigit(0x3a) = 0.
 *            isAsciiDigit(0x05) = 0.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 15
 *   Rating: 3
 */
int isAsciiDigit(int x) {
  return 2;
}

我们先把0x30和0x39转为二进制可以得到：110000和111001

我们试想一下如果我们输入的二进制位数是大于 6 位时那必定在右移六位后是不为 0 的，如果是小于或者等于 6 位时，那么得到的结果便是 0 ，我们引出第一个判断条件，来进行判断其二进制位数：

1
2
int check_1 = x >> 6;		    //判断返回结果是否为 0 ，来判断二进制位长
int condition_1 = ! check_1; 	//如果返回的是 0 便有可能是我们所需要的数字

接下来我们观察在这个 6 位的二进制位中两个数的开头均为0x11XXXX，于是我们再将输入的数据进行右移 4 位来与000011 ( 0x3 ) 进行异或来判断是否相等，得到第二个判断条件：

1
2
int check_2 = x >> 4;
int condition_2 = ! ( check_2 ^ 0x3 )		//如果两数相等返回的是 0 ，再取非得到 1

接下来我们需要判断的便是后 4 位的二进制位，我们如何得到后 4位的二进制数呢？我们利用&同为 1 下结果才为 1 的性质与0xf ( 1111 )来进行运算，得到的便是后 4 位二进制位。得到后 4 位的二进制位后我们需要的便是比较大小范围了，0x30与0x39取完后 4 位二进制位后分别为 0000和1001，题目中可使用符号并没有给出减号，需要我们自己构造一下。

1
int check_3 = x & 0xF

我们试想一下我们的二进制最大为1001 ( 9 )如果我们减去一个1010 ( 10 ) 是小于 0 的那么是不是我们所需要的数据范围？那么我们便可以写出最后一个判断表达式：

1
int condition_3 = check_3 + ( ~ 0xA + 1 )		//用 ~ A + 1 代替减号

如果减出来的值是一个负数那么得到的便是1111...，我们需要再次处理，将其右移 31 位( 因为输入最大二进制位为 32 )得到其符号位 1 ，如果减出来的数大于等于 0 其符号位为 0 ，因此我们利用符号位来判断计算结果。

1
condition_3 = !! ( condition_3 >> 31 )			//得到符号位后进行规格化，让其返回一个二进制位

于是我们将上面 3 个条件组合进行判断便可以得到对应的答案了：

1
2
3
4
5
6
7
8
9
10
int check_1 = x >> 6;		    //判断返回结果是否为 0 ，来判断二进制位长
int condition_1 = ! check_1; 	//如果返回的是 0 便有可能是我们所需要的数字

int check_2 = x >> 4;
int condition_2 = ! ( check_2 ^ 0x3 )		//如果两数相等返回的是 0 ，再取非得到 1 
    
int check_3 = x & 0xF
int condition_3 = check_3 + ( ~ 0xA + 1 )		//用 ~ A + 1 代替减号
condition_3 = !! ( condition_3 >> 31 )			//得到符号位后进行规格化，让其返回一个二进制位
return condition_1 & condition_2 & condition_3 ; //三个条件均为一个二进制位，相互 & 运算即相当于 && 运算

第七题

题目要求我们实现一个三目运算符? :

1
2
3
4
5
6
7
8
9
10
/* 
 * conditional - same as x ? y : z 
 *   Example: conditional(2,4,5) = 4
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 16
 *   Rating: 3
 */
int conditional(int x, int y, int z) {
  return 2;
}

三目运算?:中我们需要判断的便是x的值是否为 0 ，为 0 时取z的值，反之取y的值。那么有没有一种方式让我们取值时根据x的值进行返回1111...或0，让我们直接利用&运算直接取到z或y？

事实上是有的，之前我们介绍过了!!规格化一个数，如果这个数是一个 0 返回的便是 0 ，在其他情况下返回值是 1 。由于在程序中singed ( 有符号数 )执行的是算术右移 ( 填补符号位 )，而输入的最大的二进制位长 32 ，我们可以利用上述性质来进行转换出一个根据x变化而变化的数据而分别取到y或z的值。

1
2
3
int change = !! x;		//规格化 x
int num = ( x << 31 ) >> 31;		//将 x 转化为符号位，如果 change 为 0 执行后为 0 ，如果 change 为 1 执行后返回 1111...
return ( num & y ) | (( ~ num ) & z );

第八题

题目要求我们返回x和y的大小关系，如果x<=y返回 1 否则返回 0

1
2
3
4
5
6
7
8
9
10
/* 
 * isLessOrEqual - if x <= y  then return 1, else return 0 
 *   Example: isLessOrEqual(4,5) = 1.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 24
 *   Rating: 3
 */
int isLessOrEqual(int x, int y) {
  return 2;
}

这个题目中如果我们直接采用x-y的方式来编写的话，可能会造成溢出现象，我们需要考虑的是x和y两者的符号，分多种情况进行讨论。

我们先看x==y的情况，在这个情况下我们返回的是 1 ，我们可以用异或实现这个判断，如果是 0 则两数相等：

1
int condition_1 = ! ( x ^ y ) //让其相等时返回 1

第二个情况我们考虑x为+，y为-，此时我们的返回值一定是不成立的，那么要怎么判断呢？我们利用x和y的符号位来进行判断数据：

1
2
3
int signX = x >> 31 & 1;		//正数的符号位为 0 
int signY = y >> 31 & 1;		//负数的符号位为 1
int condition_2 = !(( ! signX ) & signY );

同理当x为-，y为+时：

1
int condition_3 = signX & ( ! signY )

第三个情况是两个同号时：

1
int condition_4 = ( x + ~ y + 1 ) >> 31 & 1;

我们把上面的情况合并在一起可以得到答案：

1
2
3
4
5
6
7
int condition_1 = ! ( x ^ y ) 	 //让其相等时返回 1
int signX = ( x >> 31 ) & 1;		//正数的符号位为 0 
int signY = ( y >> 31 ) & 1;		//负数的符号位为 1
int condition_2 = !(( ! signX ) & signY );
int condition_3 = signX & ( ! signY )
int condition_4 = ( x + (~ y + 1 )) >> 31 & 1;
return condition_1 | ( !condition_2 & ( condition_3 | condition_4));

第九题

题目要求我们实现!运算

1
2
3
4
5
6
7
8
9
10
11
/* 
 * logicalNeg - implement the ! operator, using all of 
 *              the legal operators except !
 *   Examples: logicalNeg(3) = 0, logicalNeg(0) = 1
 *   Legal ops: ~ & ^ | + << >>
 *   Max ops: 12
 *   Rating: 4 
 */
int logicalNeg(int x) {
  return 2;
}

对于这个题目我们需要想到的是 0 的符号位在取反前后都是 0 ，而对于一个其他不为 0 的数，在取反前后的符号位是不一样的，我们便利用这个特性来实现!：

1
2
3
int negX = ~ x + 1;
int sign = ( x | negX ) >> 31;		//x 取负后与原来的 x 的符号位进行或运算时，如果 x 为 0 返回结果则是 0 ，如果是非 0 是返回的结果是 1111... ( 执行了算术右移 )
return sign + 1;// 1111... + 1 = 0000... 利用其溢出后值为 0 的特性来进行判断

第十题

题目要我们求一个数的补码最小需要的位数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/* howManyBits - return the minimum number of bits required to represent x in
 *             two's complement
 *  Examples: howManyBits(12) = 5
 *            howManyBits(298) = 10
 *            howManyBits(-5) = 4
 *            howManyBits(0)  = 1
 *            howManyBits(-1) = 1
 *            howManyBits(0x80000000) = 32
 *  Legal ops: ! ~ & ^ | + << >>
 *  Max ops: 90
 *  Rating: 4
 */
int howManyBits(int x) {
  return 0;
}

根据题目要求我们先来判断以下这些数的值：

1
2
3
4
5
6
11111111 -> -1
1111111	 -> -1
111111	 -> -1
.
.
1		-> -1

可以看到表示一个负数时我们需要去除前面的多个 1 ，来确定表示这个数所需要的对应位数多少。同时如果输入的数据是 0 时，我们需要一个判断，来检测输入的数据是否为 0 ，如果是 0 那就可以直接返回 0 .

我们先对 0 的判断进行实现：

1
int isZero = ! x;//对 x 进行取反，如果 x 为 0 那么返回值为 1

而对于负数的符号位的个数进行判断我们需要去取其符号位，输入的二进制位最大为 32 位，所以我们将输入的数字进行左移 31 位，得到的便是其符号位。

1
int flag = x >> 31; //取其符号位

此时我们已经拥有了输入数据的符号位，我们还需要拿到输入 x 的高位，在一般其情况下我们输入的是一个正数时只需要去取出其最高位后加上一个符号位 0 ，而对于一个负数，我们需要去除前面的一连串 1 ，得到一个值的最高位为 0 ( 即其除去多余 1 后的数据 )，再加上一个符号位便是表示所需要的位数。有如下实现：

111110111 对于这个负数我们去除多余的 1 直到遇到 0 时，在加上 1 ( 代表其符号位 )

0111 ——> 4 + 1 = 5

1
x = ((~ flag ) & x ) | ( flag & ( ~ x ))	//取其最高位

我们假设一下，上面输入的一个数x是一个正数，那么有flag = 0，对于上式我们可以发现得到的新x是原来的x值即没有改变x，我们如果输入的是一个负数，那么有flag = 1而x在取反后前面多余的 1 恰好变成了 0 ，而 0 变成了 1，方便我们判断对应第一个 0 的位置。

我们已经得到了这个数的最高位，接下来需要的便是计算对应表示其二进制位个数的多少。

我们输入的数据最大的二进制位长度为 32 ，我们将其不断二分来进行判断是否需要对应长度的二进制数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int bit_16 = !!( x >> 16 ) << 4;
//截取前 16 位，如右移后的数据为 0 ，在规格化后仍为 0 ，也就不需要再左移 4 位了(乘以16，表示需要16个二进制位)
//相似的如果右移后的数据不为 0 则规格化后是 1 ，便会进行左移
x >>= bit_16;
//同理类推于截取 8、4、2、1、0 位
int bit_8 = !!( x >> 8 ) << 3;
x >>= bit_8;
int bit_4 = !!( x >> 4 ) << 2;
x >>= bit_4;
int bit_2 = !!( x >> 2 ) << 1;
x >>= bit_2;
int bit_1 = !!( x >> 1 );
x >>= bit_1;
bit_0 = x;
int result = bit_16 + bit_8 + bit_4 + bit_2 + bit_1 + bit_0 + 1;

此时我们已经拥有了输入值为 0 时的需要的二进制位和非 0 时的二进制位的个数，那么我们怎么把他们合并呢？

我们此时还是根据输入的符号位来进行处理，我们试想输入一个 0 ，那么其符号位恒为 0 ，不论在左移还是右移过程中都是不变的，而当输入一个非 0 数时，在右移过程中会有算术右移的出现，我们通过移动符号位来得到一个全为 1 ( 长 32 位 )的二级制数。那么我们在返回值时可以采用生成的全为 1 的这个数来保留我们的isZero，同时确保我们的result不会覆盖掉得到的答案，我们有如下定义：

1
2
int mask = (( !!x ) << 31 ) >> 31 ;//输入 0 时 mask 为 0
return isZero | ( mask & result );//确保了输入为 0 的时候后半截的数据为 0

把上述综合一下便是所需答案：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
int isZero = ! x;//对 x 进行取反，如果 x 为 0 那么返回值为 1  
int flag = x >> 31; //取其符号位
int mask = (( !!x ) << 31 ) >> 31 ;//输入 0 时 mask 为 0
int bit_16 , bit_8 , bit_4 , bit_2 , bit_1 , bit_0 ;

x = ((~ flag ) & x ) | ( flag & ( ~ x ))	//取其最高位
    
int bit_16 = !!( x >> 16 ) << 4;
//截取前 16 位，如右移后的数据为 0 ，在规格化后仍为 0 ，也就不需要再左移 4 位了(乘以16，表示需要16个二进制位)
//相似的如果右移后的数据不为 0 则规格化后是 1 ，便会进行左移
x >>= bit_16;
//同理类推于截取 8、4、2、1、0 位
int bit_8 = !!( x >> 8 ) << 3;
x >>= bit_8;
int bit_4 = !!( x >> 4 ) << 2;
x >>= bit_4;
int bit_2 = !!( x >> 2 ) << 1;
x >>= bit_2;
int bit_1 = !!( x >> 1 );
x >>= bit_1;
bit_0 = x;
int result = bit_16 + bit_8 + bit_4 + bit_2 + bit_1 + bit_0 + 1;

return isZero | ( mask & result );//确保了输入为 0 的时候后半截的数据为 0

第十一题

题目要求返回表达式 2*f 的位级等效值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
//float
/* 
 * floatScale2 - Return bit-level equivalent of expression 2*f for
 *   floating point argument f.
 *   Both the argument and result are passed as unsigned int's, but
 *   they are to be interpreted as the bit-level representation of
 *   single-precision floating point values.
 *   When argument is NaN, return argument
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
 *   Max ops: 30
 *   Rating: 4
 */
unsigned floatScale2(unsigned uf) {
  return 2;
}

开始前先插入一些关于浮点数的概念：

浮点数的相关二进制位的权重如图：

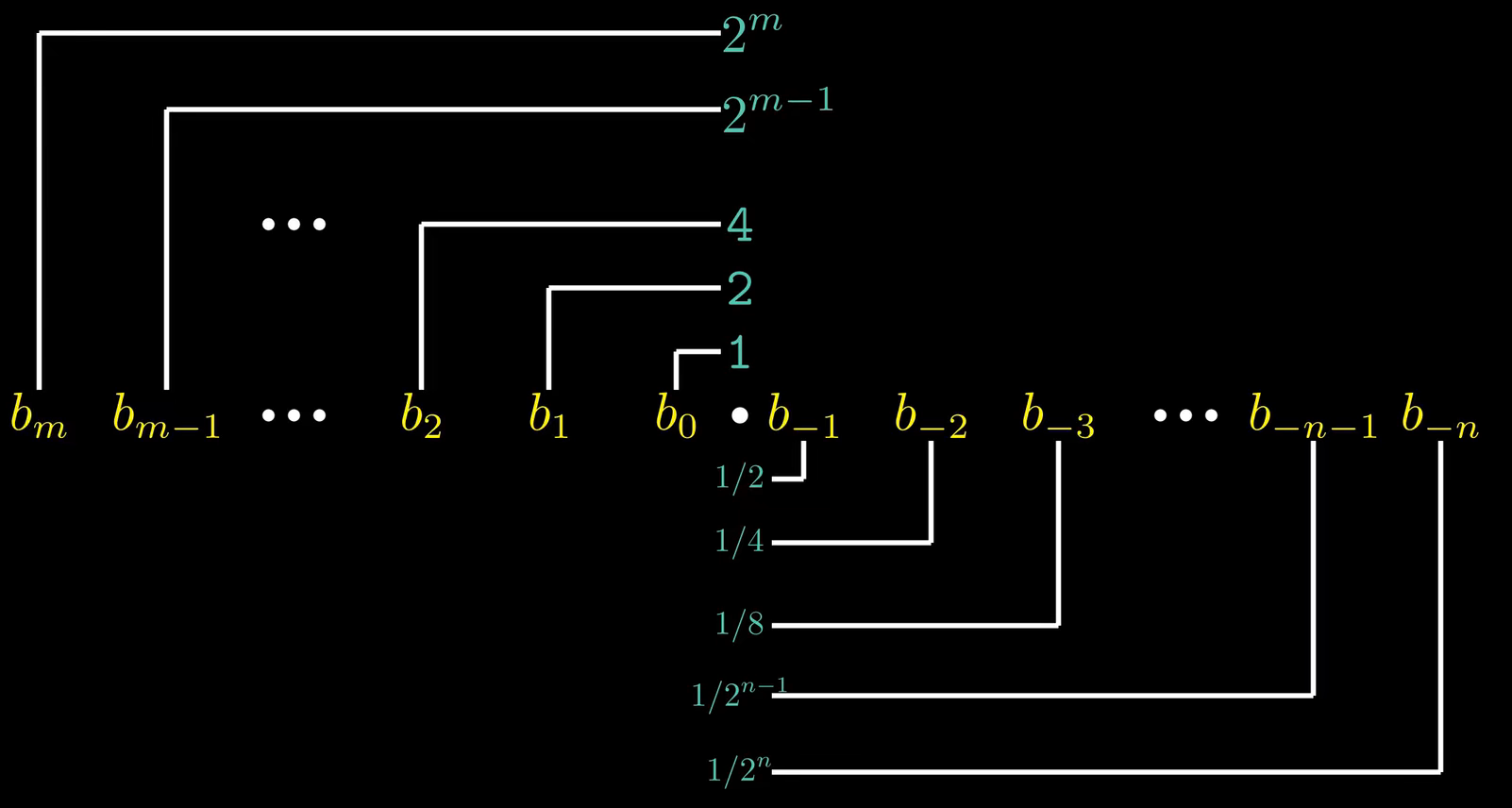
但是这个方式无法表示较大的数据，在IEEE中我们引入一个新的方式来进行表示：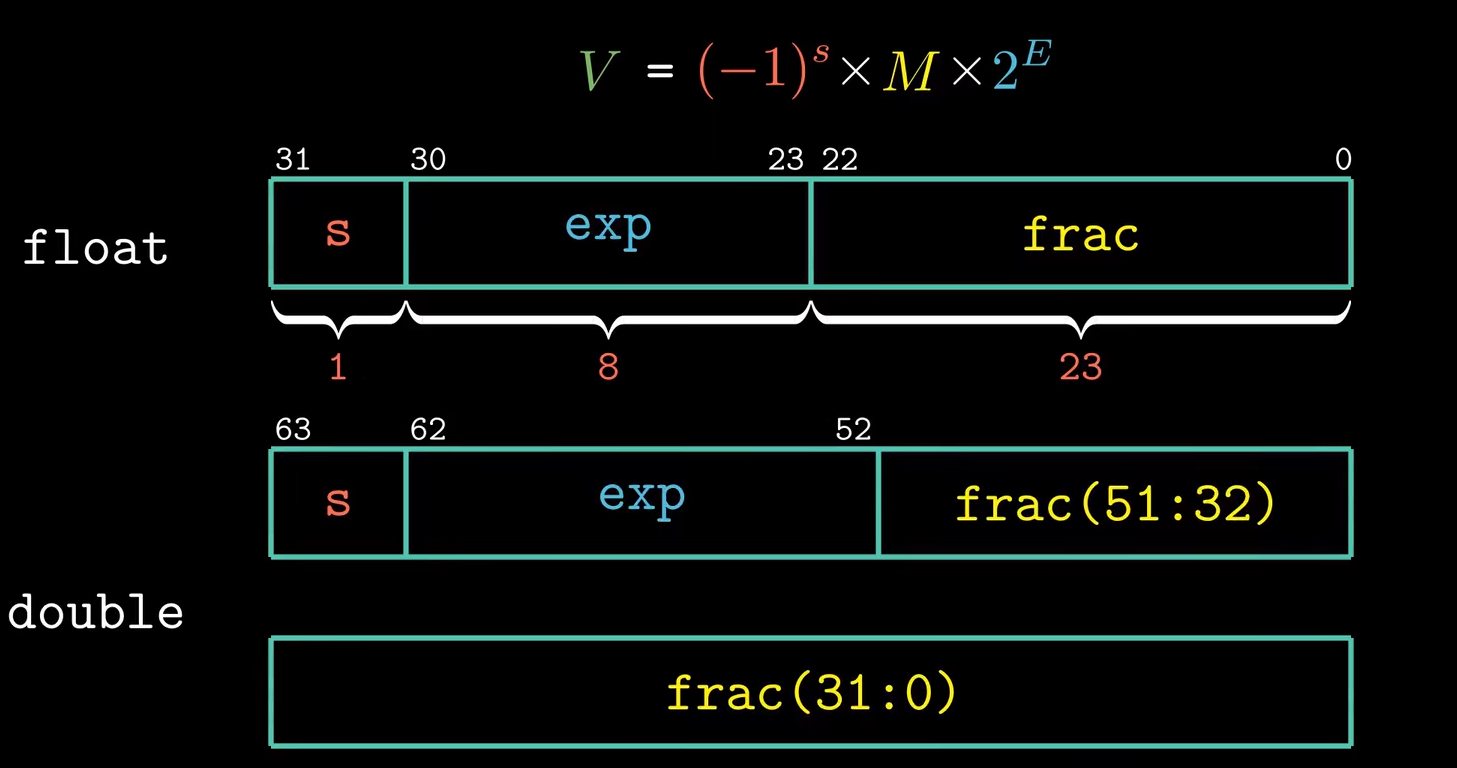

s ：符号位 | exp： 阶码 | frac：小数字段

其中数值大致可以分为三类：

  • 规格化的值

    当阶码的二进制位不全为 0 ，且不全为 1 时，此时表示的是规格化的值。

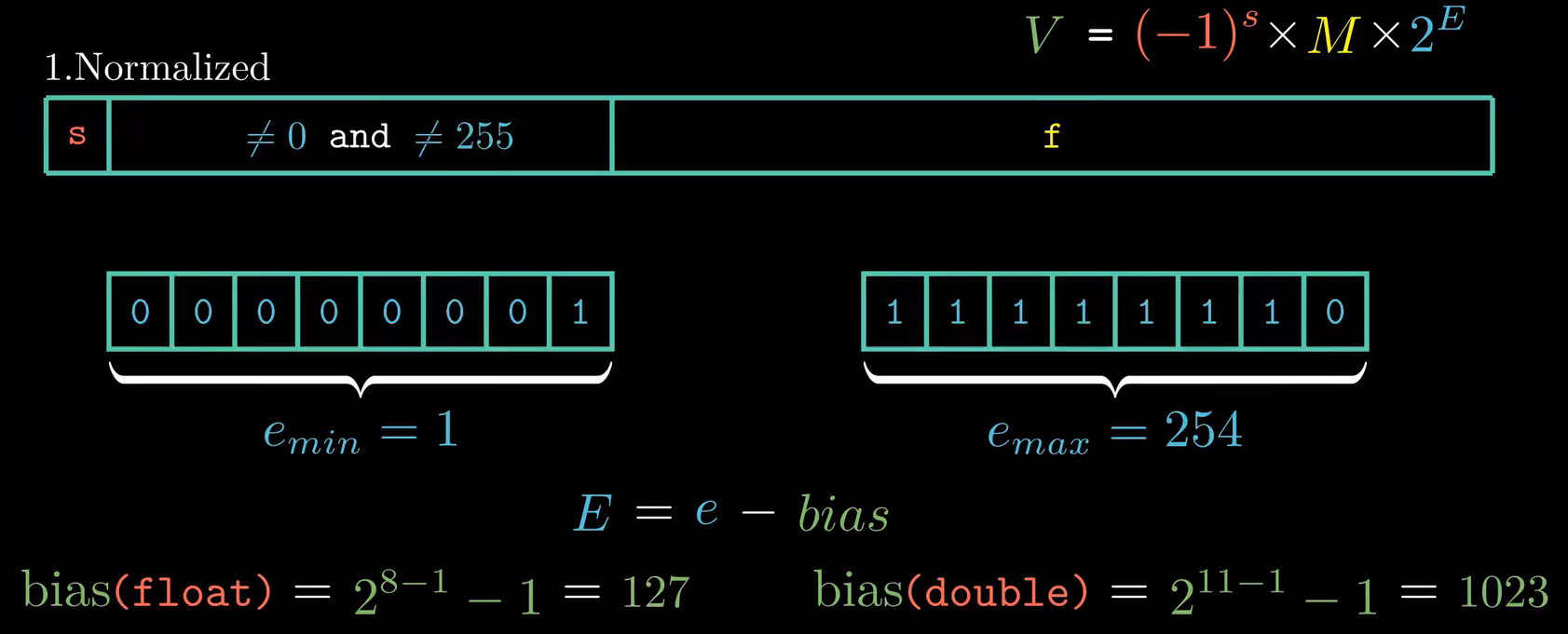
    对于图中E的值并不是解码所对应的值，而是需要其减去一个偏置，对于float和double的偏置是不相同的，则以float为例，其最小最大 E 值如下：$E_{min}=-126\ \ \ \ | \ \ \ \ E_{max}=127$

在小数字段上，尾数 M 被定义为 1+f，尾数的二进制表示如图：

因为我们可以调整 E 的取指，使得尾数 M 的取值范围大于等于 1 ，小于 2 ，既然第一位总是一，那么就没有必要显示的表示出来，这也就是为什么尾数 M 的值需要加一。

  • 非规格化的值

    当阶码的二进制位全为 0 时，此时表示的是非规格化的值。其大概有两个用途，其一是表示 0 ，其二是表示非常接近 0 的数。

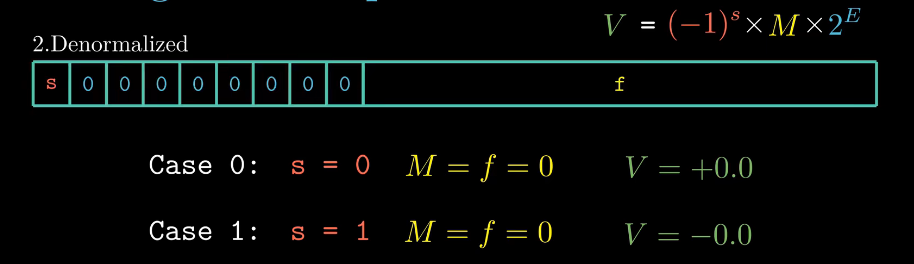
    若表示非常接近 0 的数，则阶码字段全为 0 ，阶码 E 的值等于E = 1 - bias, 尾数 M 的值是 f ( M = f )。

    +0.0 和 -0.0 在某些方面认为时不同的，而在其他方面是相同的。

  • 特殊值

    当阶码的二进制位全为 1 时，表示的数值是特殊值。特殊值分为两类，一类表示无穷大或者无穷小，另外一类表示不是一个数。

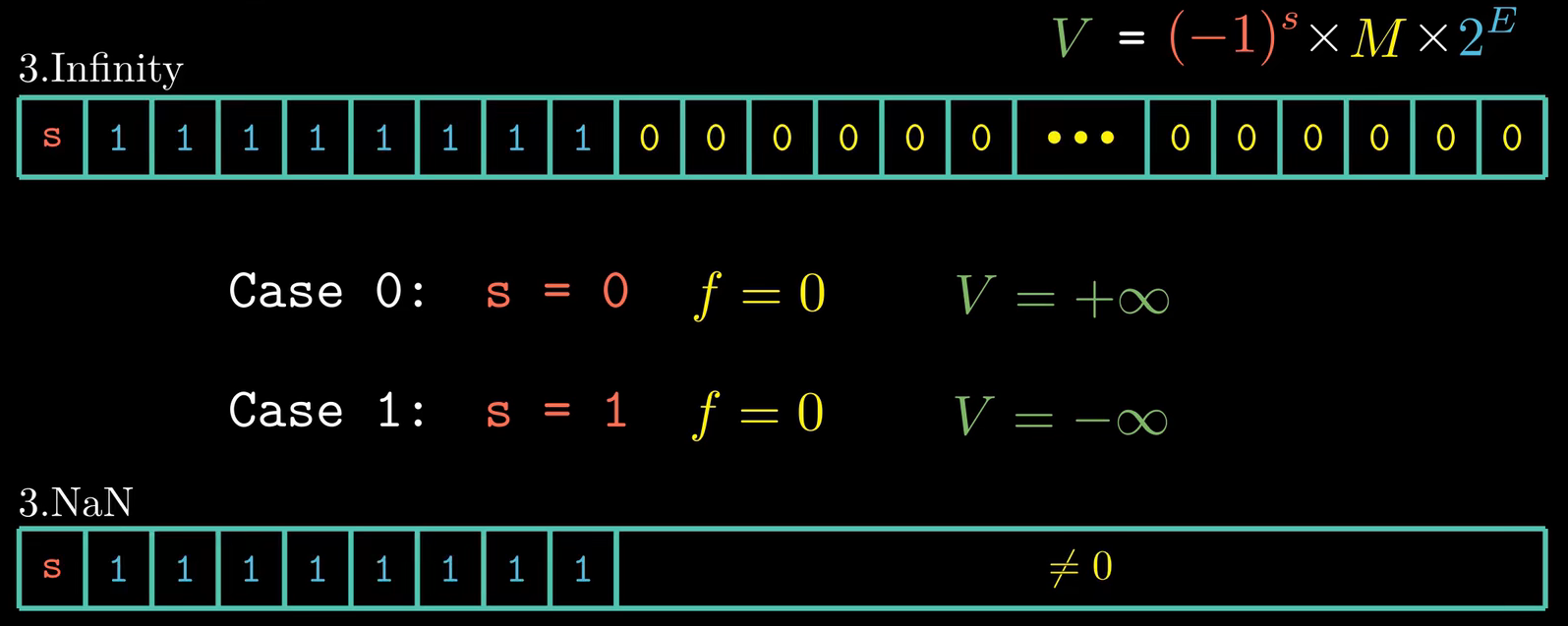
​ 如我们输出下列数据，得到的返回值便是 NaN (不是一个数)，如：$\sqrt{-1}\ \ \ \ | \ \ \ \ \infty-\infty$

了解完后题目中所给出的数据是float类型，那么我们分别去取出其s、exp、frac，便有如下计算过程：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
unsigned s = uf >> 31;
unsigned exp = (uf >> 23) & 0xFF;
unsigned frac = (uf & 0x7FFFFF);
//输入为 0
if(exp == 0 && frac ==0){
    return uf;
}

//输入为无穷或者不是一个数
if(exp == 0XFF){
    return uf;
}

//输入为非规格化的数
if(expr == 0){
	// E = exp -127 = -127
    frac <<= 1;
    return ( s << 31 ) | frac ;
}

//输入为规格化的数
exp ++;
// E = exp - 127
return ( s << 31 ) | ( exp << 23 ) | frac ;

第十二题

题目要求将浮点数转换为整数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
 /* 
 * floatFloat2Int - Return bit-level equivalent of expression (int) f
 *   for floating point argument f.
 *   Argument is passed as unsigned int, but
 *   it is to be interpreted as the bit-level representation of a
 *   single-precision floating point value.
 *   Anything out of range (including NaN and infinity) should return
 *   0x80000000u.
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
 *   Max ops: 30
 *   Rating: 4
 */
int floatFloat2Int(unsigned uf) {
  return 2;
}

与上面一个题相似，我们分别去取出其s、exp、frac，便有如下计算过程：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
unsigned s = uf >> 31;
unsigned exp = (uf >> 23) & 0xFF;
unsigned frac = (uf & 0x7FFFFF);

//输入为0 
if( exp == 0 && frac ==0 ){
	return 0;
}

//输入为无穷或者不是一个数
if( exp == 0xFF ){
	return 1 << 31;
}

//输入为非规格化的数
if( exp == 0 ){
	//E = 1 - 127 = -126
	return 0;
}

//输入为规格化的数
int E = exp - 127;
frac = frac  | ( 1 << 23 );

if( E > 31 ){
	return 1 << 31;
}else if ( E < 0 ){
    return 0;
}
//M * 2^E
if( E >= 23 ){
    frac <<= ( E - 23); 
}else{
	frac >>= ( 23 - E );
}

if(s){
	return ~ frac + 1 ;
}
return frac;

第十三题

题目要求返回对应数等于 2 的x次阶乘

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/* 
 * floatPower2 - Return bit-level equivalent of the expression 2.0^x
 *   (2.0 raised to the power x) for any 32-bit integer x.
 *
 *   The unsigned value that is returned should have the identical bit
 *   representation as the single-precision floating-point number 2.0^x.
 *   If the result is too small to be represented as a denorm, return
 *   0. If too large, return +INF.
 * 
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. Also if, while 
 *   Max ops: 30 
 *   Rating: 4
 */
unsigned floatPower2(int x) {
    return 2;
}

对于这个题目我们需要先找到对应的范围来进行判断

对于非规格化的数：

1
2
lowerbound: 2^ -149
upperbound: 2^ -126 ( 2^ -1 + 2^ -2 + ... + 2^ -23 )

对于规格化的数：

1
2
lowerbound: 2^ -126
upperbound: 2^ 127

对此我们可以写出如下操作：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
if( x < -149 ){
	return 0;
}else if( x < -126 ){
	//E = x
	//E = 1 - 127 = -126 
    int shift = 23 + ( x + 126 );
    return 1 << shift;
}else if( x <= 127 ){
	//x= exp -bias
	int exp = x + 127;
	return exp <<23;
}else{
	return ( 0XFF ) << 23;
}
Labs
CSAPP - Data Lab
https://equinox-shame.github.io/2022/03/14/Data Lab/
作者
梓曰
发布于
2022年3月14日
许可协议